Preliminary Knowledge#
条件概率公式#
条件概率的一般形式:
$$ P(A,B,C)=P(C|B,A)P(B,A)=P(C|B,A)P(B|A)P(A) $$$$P(B,C|A)=P(C|B,A)P(B|A)$$
马尔可夫条件:下一状态的概率分布只能由当前状态决定,与前面的状态无关。
$$ P(A,B,C)=P(C|B)P(B|A)P(A) $$$$ P(B,C|A)=P(C|B)P(B|A) $$
KL散度#
KL散度是衡量两个概率分布之间差异的一种度量方法,它衡量了从一个分布到另一个分布所需的额外信息。KL散度的定义是建立在熵Entropy的基础上的,熵Entropy的定义如下:
$$H(X)=-\sum_{i=1}^{n}p_i\log p_i$$
规定当$p_i=0$时,$p_i\log p_i=0$
$$H(p,q)=-\sum_{i=1}^{n}p(x)\log q(x)$$
在信息论中,交叉熵可认为是对预测分布$q(x)$用真实分布$p(x)$来进行编码时所需要的信息量大小
因此我们可以通过交叉熵和信息熵来推到相对熵即KL散度:
$$
\begin{align}
D_{KL}(p||q)&=H(p,q)-H(p) \nonumber\\
&=-\sum_{i=1}^{n}p(x)\log q(x)+\sum_{i=1}^{n}p(x)\log p(x) \nonumber\\
&=-\sum_{i=1}^{n}p(x)\log \frac{q(x)}{p(x)} \nonumber
\end{align}
$$
KL散度的特点:
- 非对称性:$D_{KL}(p||q)\neq D_{KL}(q||p)$
- 非负性:$D_{KL}(p||q)\geq 0$
$$
\begin{align}
p(x)&=\frac{1}{\sqrt{2\pi}\sigma_1}exp({-\frac{(x-\mu_1)^2}{2\sigma_1^2}}) \nonumber\\
q(x)&=\frac{1}{\sqrt{2\pi}\sigma_2}exp({-\frac{(x-\mu_1)^2}{2\sigma_2^2}}) \nonumber
\end{align}
$$$$
\begin{align}
\int p(x)\log(p(x))dx &= -\frac{1}{2}[1+\log(2\pi\sigma_1^2)] \nonumber\\
\int p(x)\log(q(x))dx &= -\frac{1}{2}\log(2\pi\sigma_2^2)-\frac{\sigma_1^2+(\mu_1-\mu_2)^2}{2\sigma_2^2} \nonumber\\
\end{align}
$$$$
\begin{align}
D_{KL}(p||q)&=\log\frac{\sigma_2}{\sigma_1}+\frac{\sigma_1^2+(\mu_1-\mu_2)^2}{2\sigma_2^2}-\frac{1}{2} \nonumber\\
\end{align}
$$
高斯分布的重参数化#
若希望从高斯分布中采样,我们可以使用标准正态分布$\mathcal{N}(0,1)$来采样$z$,然后通过重参数化$\sigma*z+\mu$的方式将其转换为高斯分布$N(\mu,\sigma^2)$。
这样做的好处在于将随机性转移到了$z$这个常量上,使得采样过程梯度可传播,从而可以使用梯度下降等优化算法进行训练。
VAE与多层VAE#
单层VAE#
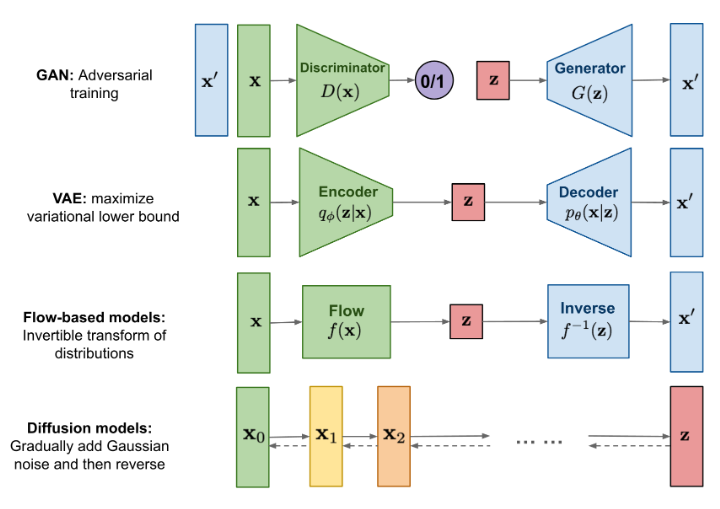
$$p(x)=\int_{z} p(x, z)$$$$p(x)=\int_{z} p_{\theta}(x|z)p(z)$$$$p(x)=\int_{z} q_{\phi}(z|x)\frac{p_{\theta}(x|z)p(z)}{q_{\phi}(z|x)}$$$$\begin{align}
\log p(x)&=\log \int_{z} q_{\phi}(z|x)\frac{p_{\theta}(x|z)p(z)}{q_{\phi}(z|x)} \nonumber\\
&=\log \mathbb{E}_{z\sim q_{\phi}(z|x)}\frac{p_{\theta}(x|z)p(z)}{q_{\phi}(z|x)}\nonumber\\
\end{align}
$$$$\begin{align}
logp(x)&\ge \mathbb{E}_{z\sim q_{\phi}(z|x)}\left [\log \frac{p_{\theta}(x|z)p(z)}{q_{\phi}(z|x)} \right ] \nonumber\\
&=\mathbb{E}_{z\sim q_{\phi}(z|x)}[\log p_{\theta}(x|z)]-\mathbb{E}_{z\sim q_{\phi}(z|x)}\left [\log \frac{q_{\phi}(z|x)}{p(z)}\right ] \nonumber\\
&= \mathbb{E}_{z\sim q_{\phi}(z|x)}[\log p_{\theta}(x|z)]-D_{KL}(q_{\phi}(z|x)||p(z)) \nonumber\\
\end{align}$$
第一项为重建项,第二项为正则化项。
多层VAE#
…(updating)
Diffusion Models#
…(updating)
