Preliminary Knowledge
条件概率公式
条件概率的一般形式:
$$ P(A,B,C)=P(C|B,A)P(B,A)=P(C|B,A)P(B|A)P(A) $$
$$ P(B,C|A)=P(C|B,A)P(B|A) $$
马尔可夫条件:下一状态的概率分布只能由当前状态决定,与前面的状态无关。
$$ P(A,B,C)=P(C|B)P(B|A)P(A) $$
$$ P(B,C|A)=P(C|B)P(B|A) $$
KL散度
KL散度是衡量两个概率分布之间差异的一种度量方法,它衡量了从一个分布到另一个分布所需的额外信息。KL散度的定义是建立在熵 Entropy 的基础上的,熵的定义如下:
$$ H(X)=-\sum_{i=1}^{n}p_i\log p_i $$
规定当 $p_i=0$ 时,$p_i\log p_i=0$
$$ H(p,q)=-\sum_{i=1}^{n}p(x)\log q(x) $$
在信息论中,交叉熵可认为是对预测分布 $q(x)$ 用真实分布 $p(x)$ 来进行编码时所需要的信息量大小。因此我们可以通过交叉熵和信息熵来推导相对熵(KL散度):
$$ \begin{align} KL(p\parallel q)&=H(p,q)-H(p) \\ &=-\sum_{i=1}^{n}p(x)\log q(x)+\sum_{i=1}^{n}p(x)\log p(x) \\ &=-\sum_{i=1}^{n}p(x)\log \frac{q(x)}{p(x)} \end{align} $$
KL散度的特点:
- 非对称性:$KL(p\parallel q)\neq KL(q\parallel p)$
- 非负性:$KL(p\parallel q)\geq 0$
如果固定$p(x)$,那么$KL(p\parallel q)=0 \Leftrightarrow p(x)=q(x)$。实际上这一点的证明要用到变分法,也是VAE中V的由来。
$$ \begin{align} p(x)&=\frac{1}{\sqrt{2\pi}\sigma_1}\exp\left({-\frac{(x-\mu_1)^2}{2\sigma_1^2}}\right) \\ q(x)&=\frac{1}{\sqrt{2\pi}\sigma_2}\exp\left({-\frac{(x-\mu_1)^2}{2\sigma_2^2}}\right) \end{align} $$
$$ \begin{align} \int p(x)\log(p(x))dx &= -\frac{1}{2}\left[1+\log(2\pi\sigma_1^2)\right] \\ \int p(x)\log(q(x))dx &= -\frac{1}{2}\log(2\pi\sigma_2^2)-\frac{\sigma_1^2+(\mu_1-\mu_2)^2}{2\sigma_2^2} \end{align} $$
$$ KL(p\parallel q)=\log\frac{\sigma_2}{\sigma_1}+\frac{\sigma_1^2+(\mu_1-\mu_2)^2}{2\sigma_2^2}-\frac{1}{2} $$
高斯分布的重参数化
若希望从高斯分布中采样,我们可以使用标准正态分布 $\mathcal{N}(0,1)$ 来采样 $z$,然后通过重参数化 $\sigma*z+\mu$ 的方式将其转换为高斯分布 $N(\mu,\sigma^2)$。
这样做的好处在于将随机性转移到了 $z$ 这个常量上,使得采样过程梯度可传播,从而可以使用梯度下降等优化算法进行训练。
生成模型
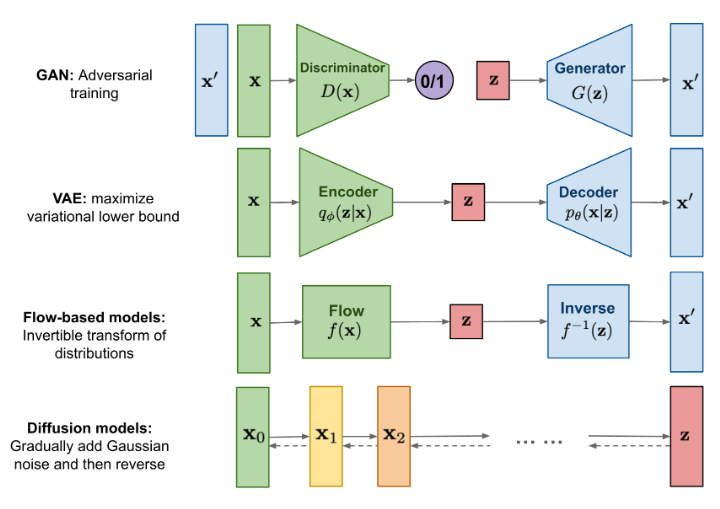
VAE
首先我们先回顾一下VAE在干什么:
我们有一批数据样本${x_1,x_2,…,x_n}$,对这个整体我们用$x$描述,我们的理想情况是得到$x$的分布$\tilde{p}(x)$,这样我们就可以直接根据$\tilde{p}(x)$来采样得到所有可能的$x$了,但是这显然很难实现。因此我们引入了$z$,$z$服从标准正态分布$\mathcal{N}(0,I)$,也就是说,我们可以先从标准正态分布中采样一个$z$,然后训练一个模型$q_{\theta}(x|z)$来算出$x$,用苏神的图解释该过程
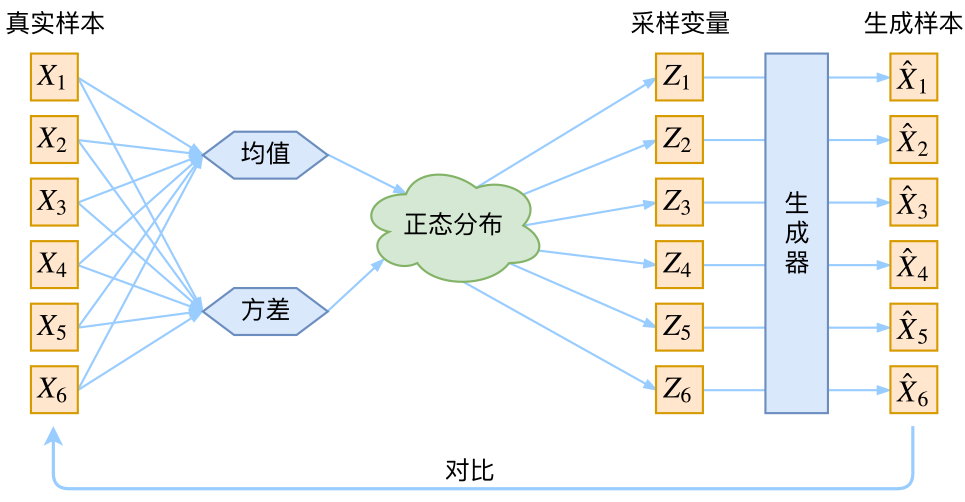
$$ q(x)=\int q_{\theta}(x|z)q(z)dz $$
$$ q(x, z)= q(x|z)q(z) $$
但是,实际上这个过程是存在问题的,我们并不清楚在标准正态分布中采样得到$z_{k}$是否对应原来的$x_{k}$,因此,我们不能简单地最小化$x_{k}$和$\hat{x}_{k}$之间的距离。
实际上在VAE中,我们假设的是后验分布$p(z|x)$为正态分布,也就是说,给定一个样本$x_k$,我们假设存在一个专属于$x_k$的分布$p(z|x_k)$,并且假设其为正态分布。这样我们从这个分布中采样出来的$z_k$可以确定是与$x_k$对应的。
那么如何得到这个专属的分布呢?既然已经假设他是一个正态分布了,那我们就只要知道他的均值$\mu$ 和方差$\sigma^2$就行了。怎么算均值和方差呢?那就用神经网络拟合出来吧!
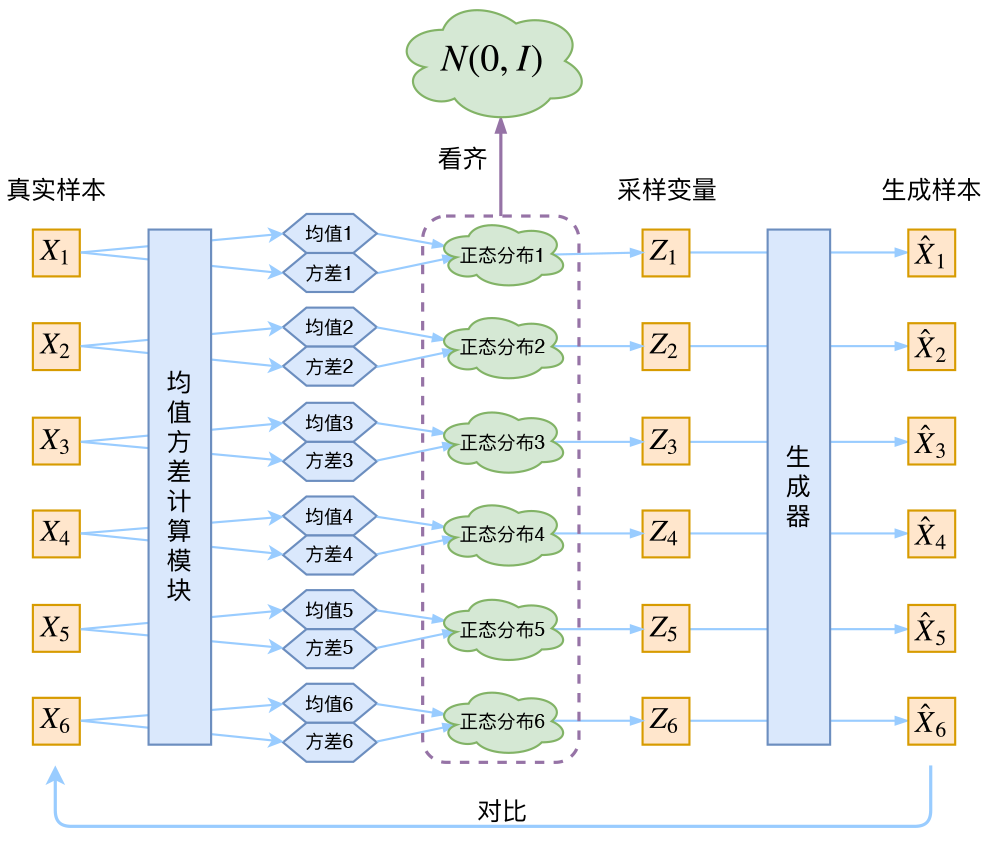
如何优化呢?我们的目标是希望$q(x)$能够逼近$\tilde{p}(x)$,这样的话就可以利用KL散度。具体来说,我们用$q(x,z)$来逼近$p(x,z)=\tilde{p}(x)p(z|x)$:
$$ KL(p(x,z)\parallel q(x,z)) = \int\int p(x,z)\ln\frac{p(x,z)}{q(x,z)}dzdx $$
$$ \begin{align} KL(p(x,z)\parallel q(x,z)) &= \int\tilde{p}(x)\left [\int p(z|x)\ln\frac{p(x,z)}{q(x,z)}dz\right ]dx \\ &=\mathbb{E}_{x\sim \tilde{p}(x)}\left [\int p(z|x)\ln\frac{p(x,z)}{q(x,z)}dz\right ] \end{align} $$
进一步省略$\tilde{p}(x)$带来的常数项:
$$ \mathcal{L} = KL(p(x,z)\parallel q(x,z)) = \mathbb{E}_{x\sim \tilde{p}(x)}\left[\int p(z|x)\ln\frac{p(x|z)}{q(x,z)}dz\right] $$
再将 $q(x, z)= q(x|z)q(z)$ 代入,有:
$$ \mathcal{L} = \mathbb{E}_{x\sim \tilde{p}(x)} \left [\mathbb{E}_{z\sim p(z|x)}[-\ln q(x|z)] + KL(p(z|x) \parallel q(z))\right ] $$
因此,我们目标就是优化 $q(x|z)$ 和 $q(z)$ 使得 $\mathcal{L}$ 最小化。
在代码实现过程中,$q(z)$ 假设为标准正态分布,$p(z|x),q(x|z)$ 分别对应Encoder和Decoder部分,都是未知的,这里我们都用神经网络来进行拟合。
首先对于 $p(z|x)$ ,我们假设其为均值为 $\mu(x)$,方差为 $\sigma^2(x)$ 的正态分布,$\mu(x)$ 和 $\sigma^2(x)$ 为输入为 $x$ ,输出为均值和方法的神经网络。因此loss中的KL散度项可以计算出来:
$$ KL(p(z|x)\parallel q(z)) = \frac{1}{2}\sum^{d}_{k=1}(\mu^2_{(k)}(x)+\sigma^2_{(k)}(x)-\ln\sigma^2_{(k)}(x)-1) $$
对于 $q(x|z)$ ,VAE论文给出了两种分布:伯努利分布以及正态分布,我们仍然以正态分布为例,仍然依靠神经网络估计均值和方差,$\tilde{\mu}(z)$,$\tilde{\sigma}^2(z)$,但是在这里我们通常会将方差固定为常数 $\tilde{\sigma}^2$ ,因此:
$$ -\ln q(x|z) \sim \frac{1}{2\tilde{\sigma}^2}||x-\tilde{\mu}(z)||^2 $$
在VAE中我们从 $p(z|x)$ 采样一个样本进行训练,那么也就是说:
$$ \mathcal{L} = \mathbb{E}_{x\sim \tilde{p}(x)}\left [-\ln q(x|z) + KL(p(z|x) \parallel q(z))\right ] $$
这样训练的loss也就能精确的计算出来了。
Diffusion Models
主要参考了Lil’s Log,苏神的生成扩散模型漫谈系列
DDPM
前向扩散过程(加噪)
Given a data point sampled form a real data distribution $x_0 \sim q(x)$, we define a forward diffusion process: we add small amount of Gaussian noise to the sample in $T$ steps, producing a sequence of noisy samples $x_1,…,x_T$. The step sizes are controlled by a variance schedule ${\beta_{t}\in(0,1)}_{t=1}^{T}$.
$$ \begin{align} q(x_t|x_{t-1}) &= \mathcal{N}(x_t; \sqrt{1-\beta_t}x_{t-1}, \beta_t I) \\ q(x_{1:T}|x_0) &= \prod_{t=1}^{T}q(x_t|x_{t-1}) \end{align} $$
这里的前向过程可以视为马尔可夫过程,即当前状态$x_t$只与上一时刻的状态$x_{t-1}$有关。在给定上一状态$x_{t-1}$的条件下,获取第$t$步样本$x_t$的概率分布q(x_t|x_{t-1})。$\mathcal{N}(x_t; \sqrt{1-\beta_t}x_{t-1}, \beta_t I)$ 表示给定上一步的状态$x_{t-1}$, $x_{t}$是一个以$\sqrt{1-\beta_t}x_{t-1}$为均值, $\beta_t I$为协方差的高斯分布的随机变量.
也就是说:$x_{t} = \sqrt{\alpha_t}x_{t-1}+\sqrt{1-\alpha_{t}}\epsilon_{t-1}, \epsilon_{t-1}\in\mathcal{N}(0,I)$
因此,当步数$t$逐渐增大时,采样数据$x_0$会逐渐趋向于纯高斯噪声
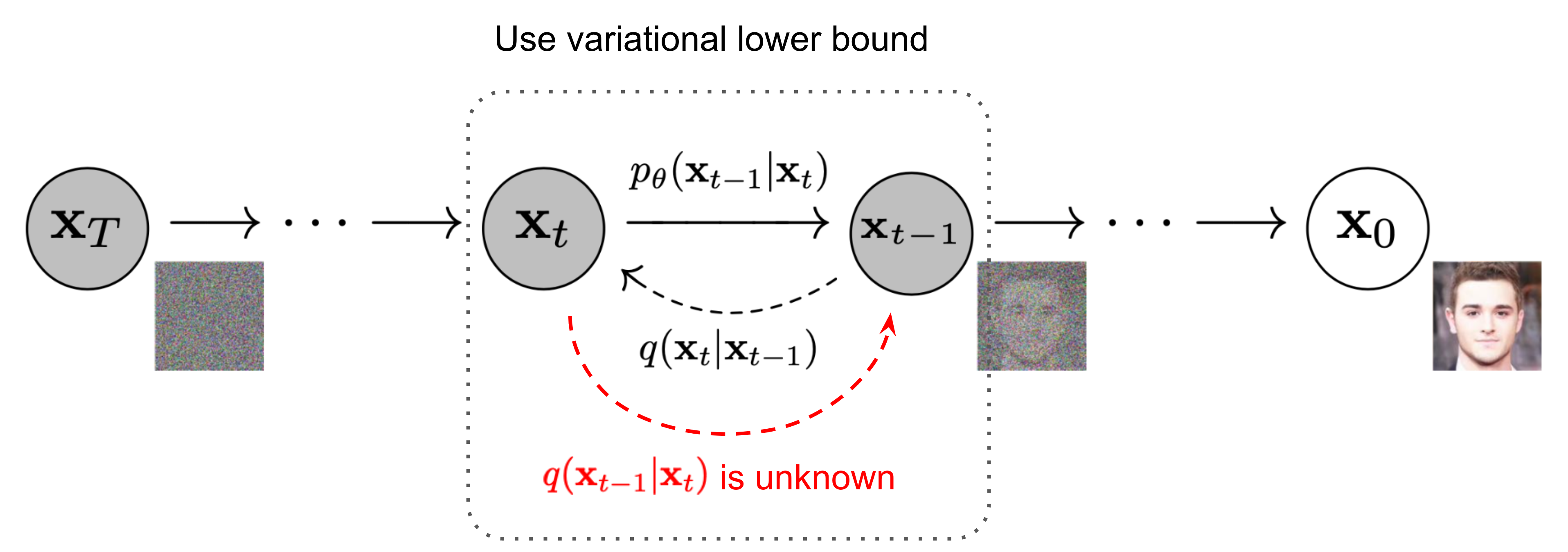
At any arbitrary time step $t$, we can sample $x_t$ in above process. Let $\alpha_{t} = 1-\beta_{t}$, $\bar{\alpha}_{t} = \prod_{i=1}^{t}\alpha_{i}$ and $\bar{\beta}_{t} = \sqrt{1-\bar{\alpha}_{t}^2}$:
$$ \begin{align} x_{t} &= \sqrt{\alpha_t}x_{t-1}+\sqrt{1-{\alpha}_{t}}\epsilon_{t} \\ \nonumber &=\sqrt{\alpha_t\alpha_{t-1}}x_{t-2}+\sqrt{1-\alpha_{t}\alpha_{t-1}}\epsilon_{t-2} \\ \nonumber &=… \\ \nonumber &=\sqrt{\bar{\alpha}_{t}}x_{0}+\sqrt{1-\bar{\alpha}_{t}}\epsilon \\ q(x_t|x_0) &= \mathcal{N}(x_t; \sqrt{\bar{\alpha}_{t}}x_{0}, (1-\bar{\alpha}_{t})I) \end{align} $$
反向扩散过程(去噪)
If we can reverse the forward process and sample from $q(x_{t-1}|x_t)$, we will be able to recreate the true sample form a Gaussian noise input, $x_{T} \sim \mathcal{N}(0,I)$. Unfortunately, we cannot easily estimate $q(x_{t-1}|x_t)$ because it needs to use the entire dataset and therefore we need to learn a model $p_{\theta}$ to approximate these conditional probabilities in order to run the reverse diffusion process.
$$ \begin{align} p_{\theta}(x_{0:T}) &= p(x_T)\prod_{i=1}^{t}p_{\theta}(x_{t-1}|x_t) \\ p_{\theta}(x_{t-1}|x_t) &= \mathcal{N}(x_{t-1};\mu_{\theta}(x_t,t), \Sigma_{\theta}(x_t,t)) \end{align} $$
如何学习这一过程呢?最简单的方法就是最小化$x_{t-1}$和$p_{\theta}(x_{t-1}|x_t)$之间的欧式距离:
$$ ||x_{t-1}-p_{\theta}(x_{t-1}|x_t)||^{2} $$
继续细化这一过程,将前向过程可以改写为$x_{t-1}=\frac{1}{\sqrt{\alpha_t}}(x_t-\sqrt{1-\alpha_{t}}\epsilon_{t})$,因此模型$p_{\theta}$可以设计为:
$$ p_{\theta}(x_{t-1}|x_t) = \frac{1}{\sqrt{\alpha_t}}(x_t-\sqrt{1-\alpha_{t}}\epsilon_{\theta}(x_t,t)) $$
代入训练损失函数:
$$ ||x_{t-1}-p_{\theta}(x_{t-1}|x_t)||^{2} = \frac{\beta_{t}}{\alpha_t}||\epsilon_{t}-\epsilon_{\theta}(x_t,t)||^{2} $$
忽略常数系数 $\frac{\beta_{t}}{\alpha_t}$,然后代入 $x_{t} = \sqrt{\bar{\alpha}_{t}}x_{0}+\sqrt{1-\bar{\alpha}_{t}}\epsilon$,最终得到的损失函数:
$$ ||\epsilon_{t}-\epsilon_{\theta}(\sqrt{\bar{\alpha}_{t}}x_{0}+\sqrt{1-\bar{\alpha}_{t}}\epsilon_{t},t)||^{2} $$
DDIM
我们也可以用贝叶斯重新认识DDPM的过程:
正向过程每一步是 $x_{t} = \sqrt{\alpha_t}x_{t-1}+\sqrt{1-\alpha_{t}}\epsilon_{t-1}, \epsilon_{t-1}\in\mathcal{N}(0,I)$,可以求出 $q(x_t|x_0) = \mathcal{N}(x_t; \sqrt{\bar{\alpha}_{t}}x_{0}, (1-\bar{\alpha}_{t})I)$。DDPM要做的事就是从正向过程中求出反向过程所需要的 $q(x_{t-1}|x_t)$,这样就可以实现从任意 $x_T=z$ 出发,逐步采样出$x_{T-1}, x_{T-2}, …$ 一直到 $x_0$。
那么,根据贝叶斯定理,我们有:
$$ q(x_{t-1}|x_{t}) = \frac{q(x_{t}|x_{t-1})q(x_{t-1})}{q(x_t)} $$
我们不知道 $q(x_{t-1})$ 和 $q(x_t)$ 的表达式,但是我们知道的 $x_0$,因此我们可以将 $x_0$ 加入得到:
$$ q(x_{t-1}|x_{t}, x_0) = \frac{q(x_{t}|x_{t-1})q(x_{t-1}|x_0)}{q(x_t|x_0)} $$
这样公式的每一项我们都是已知的,所以上式是可以计算出来的:
$$ \begin{align} q({x}_{t-1}|{x}_t,{x}_0)=\mathcal{N}\left({x}_{t-1};\frac{\alpha_t\bar{\beta}_{t-1}^2}{\bar{\beta}_t^2}{x}_t+\frac{\bar{\alpha}_{t-1}\beta_t^2}{\bar{\beta}_t^2}{x}_0,\frac{\bar{\beta}_{t-1}^2\beta_t^2}{\bar{\beta}_t^2}{I}\right) \label{eq_backward} \end{align} $$
目前 $q({x}_{t-1}|{x}_t,{x}_0)$ 有两个依赖项$x_t, x_0$,但实际上 $x_0$ 是我们最终想要生成的结果,我们不能依赖 $x_0$。那么一个自然的想法是如果我们能够通过 $x_t$ 来预测 $x_0$,不就可以避免这一问题了吗?因此可以引入去噪模型 $\bar{\mu}(x_t)$ 来预测 $x_0$:
$$ \bar{\mu}(x_t) = \frac{1}{\bar{\alpha}_t}(x_t-\bar{\beta}_t\epsilon_{\theta}(x_t,t)) $$
代入 $\eqref{eq_backward}$,可以得到: $$ q({x}_{t-1}|{x}_t,{x}_0) \approx \mathcal{N}\left({x}_{t-1};\frac{1}{\alpha_t}\left(x_t-\frac{\beta_t^2}{\bar{\beta}_t}\epsilon_{\theta}(x_t, t)\right),\frac{\bar{\beta}_{t-1}^2 \beta_t^2}{\bar{\beta}_t^2}I\right) $$
虽然我们从单步正向过程 $q(x_t|x_{t-1})$ 一步步推导到 $q({x}_{t-1}|{x}_t,{x}_0)$,但是我们可以看到实际上结果与 $q(x_t|x_{t-1})$ 并没有什么关系,那么DDIM的思想就是在推导过程中舍弃掉 $q(x_t|x_{t-1})$。那么该如何求解 $q({x}_{t-1}|{x}_t,{x}_0)$ 呢?
DDIM提出用待定系数法求解,我们仍然假设 $q({x}_{t-1}|{x}_t,{x}_0)$ 为正态分布:
$$ \begin{align} q({x}_{t-1}|{x}_t,{x}_0) = \mathcal{N}\left(x_{t-1}; \kappa_{t}x_t+\lambda_{t}x_0, \sigma_{t}^2 I\right) \label{eq_ddim} \end{align} $$
并且该分布需要满足边际分布条件: $$ \int q({x}_{t-1}|{x}_t,{x}_0)q(x_t|x_0) = q(x_{t-1}|x_0) $$
想要满足该条件,其实只需要满足两个方程: $$ \begin{align} \bar{\alpha}_{t-1} &= \kappa_{t}\bar{\alpha}_{t}+\lambda_{t} \\ \bar{\beta}_{t-1} &= \sqrt{\kappa_{t}^2\bar{\beta}_{t}^2+\lambda_{t}^2} \end{align} $$
关于如何得到这两个方程,可以参考苏神生成扩散模型漫谈(四)

解这两个方程,可以得到 $\kappa_{t}$ 和 $\lambda_{t}$ 的表达式:
$$ \begin{align} \kappa_{t} &= \frac{\sqrt{\bar{\beta}_{t-1}^2-\sigma_t^2}}{\bar{\beta}_t} \\ \lambda_{t} &= \bar\alpha_{t-1}-\frac{\bar\alpha_t\sqrt{\bar{\beta}_{t-1}^2-\sigma_t^2}}{\bar{\beta}_t} \end{align} $$
可以代入 $\eqref{eq_ddim}$,同时将$x_0$替换为用$x_t$推导的形式(和DDPM一样),最终得到: $$ \begin{align} q(x_{t-1}|x_t) \approx \mathcal{N}\left({x}_{t-1};\frac{x_t-\bar\beta_t}{\alpha_t} \epsilon_{\theta}(x_t, t) + \sqrt{\bar\beta_{t-1}^2-\sigma_t^2}\epsilon_{\theta}(x_t, t),\sigma_t^2 I\right) \end{align} $$
SDE
updating…..
Conditioned Generation
Classifier Guided Diffusion
updating…..